Research

My research primarily explores the application of Calculus of Variations and spectral theory in material science, with a particular focus on understanding mechanical metamaterials -- carefully designed materials that exhibit exotic functionalities -- from a mathmatical perspective. For an overview of mechanical metamaterials, you can refer to this Nature review paper.

My current projects on mechanical metamaterials can be categorized into the following areas:

• Effective elastic behavior of mechanism-based mechanical metamaterials
• Higher-order rigid bar joint frameworks with applications to tensegrity structures
• Pseudo-magnetism in the slowly-strained discrete honeycomb lattice

• Effective elastic behavior of mechanism-based mechanical metamaterials

This project addresses problems from an emerging area of mechanics known as mechanism-based mechanical metamaterials. These materials often consist of periodically arranged building blocks, resembling elastic composites. However, compared to the traditional elastic composites, these mechanism-based mechanical metamaterials are more degenerate, since they can deform with zero elastic energy. Such deformations are called mechanisms.

One fascinating consequence of the presence of mechanisms in these metamaterials is their degenerate elastic behavior. In fact, these materials possess soft modes, which are large deformations that require only a small amount of elastic energy. Interestingly, the soft modes often result in global deformations that are entirely different from those of the mechanisms. A significant portion of my research is dedicated to developing an effective theoretical framework to study specialized mechanism-based mechanical metamaterials, where soft modes correspond to deformations that result in zero effective elastic energy.

A vivid and illustrative example for explaining our work on mechanism-based mechanical metamaterials is the Kagome lattice, which is a 2D tiling consisting of triangles and hexagons. Deriving an effective theory is not simple for the Kagome lattice since it has an infinite number of mechanisms. The following two figures show two different mechanisms of the Kagome lattice.

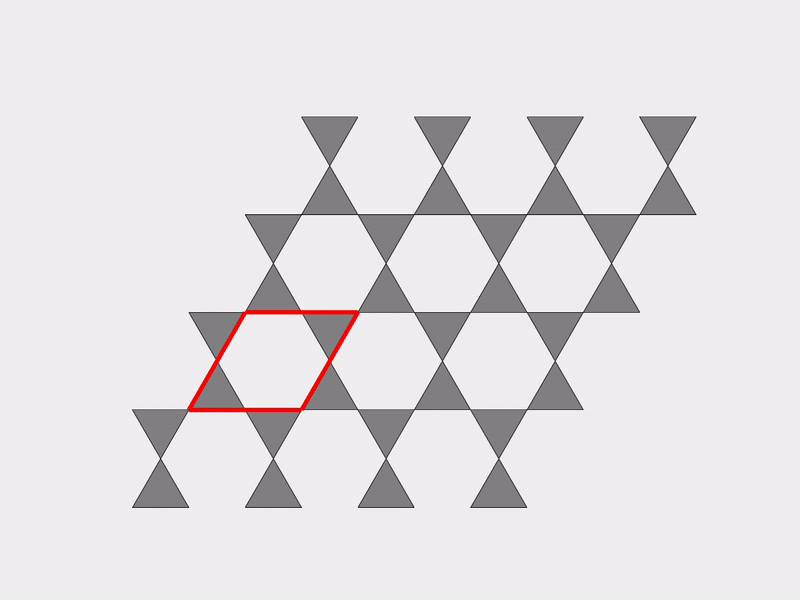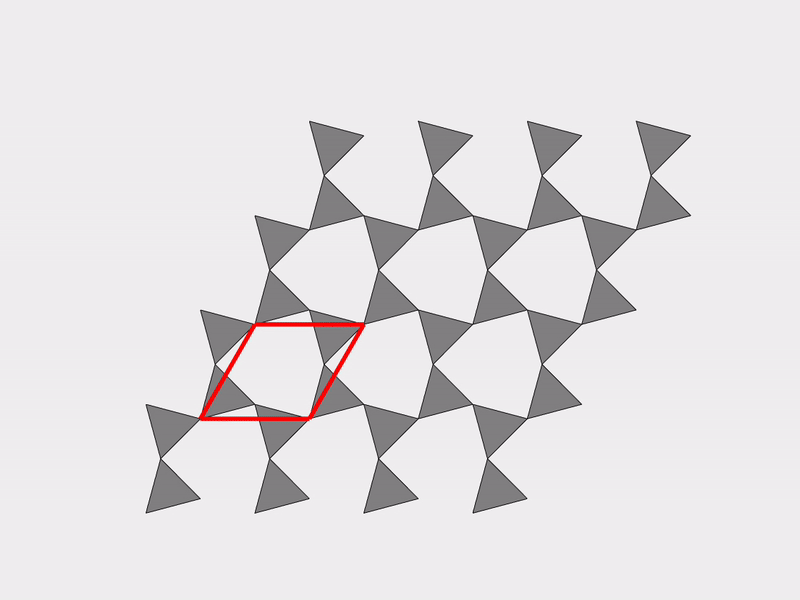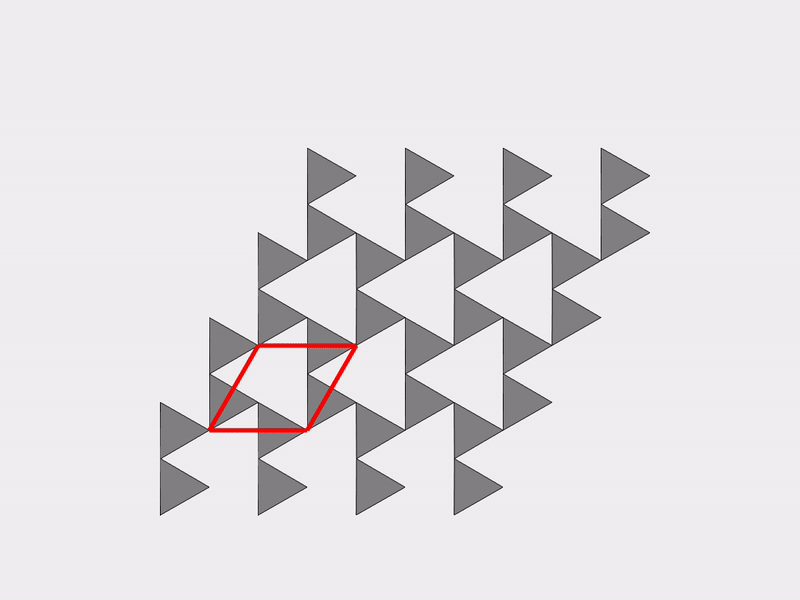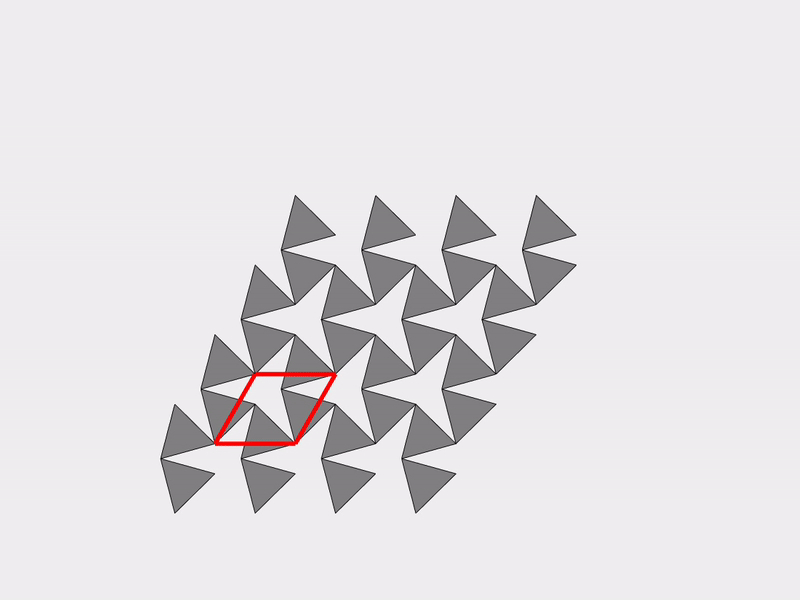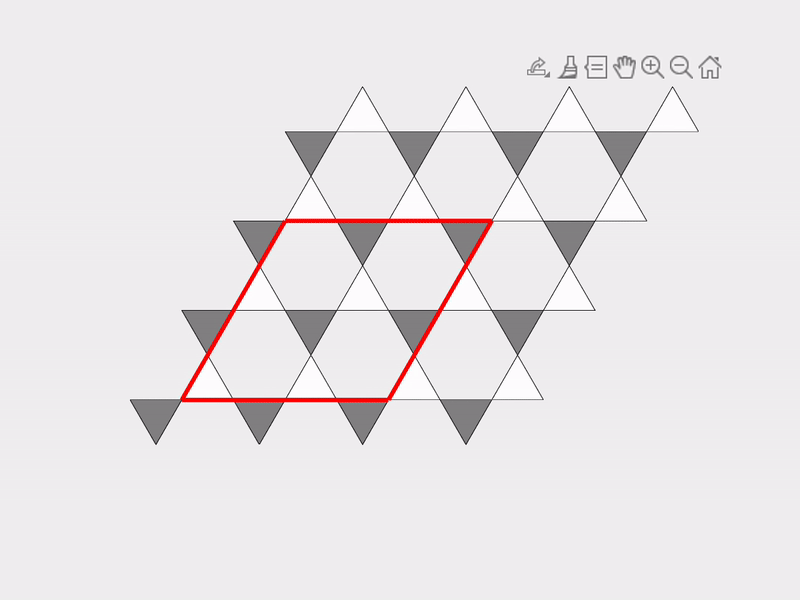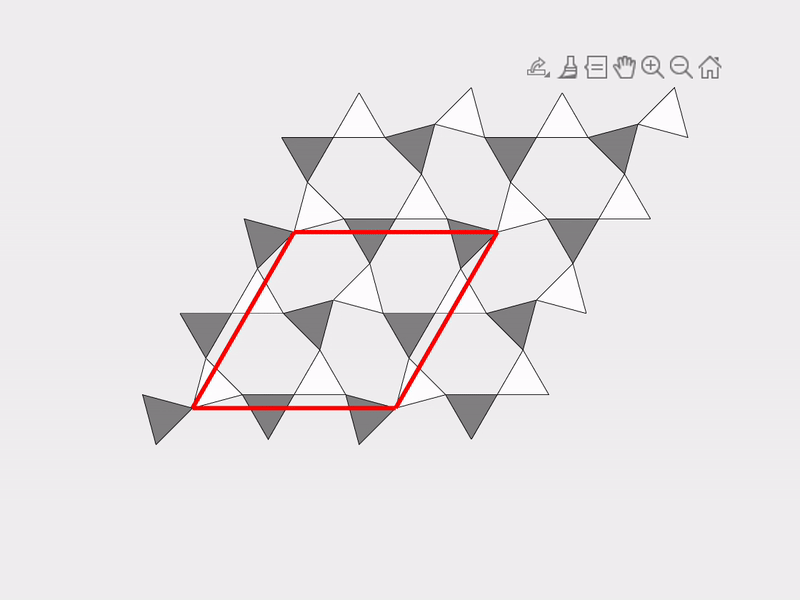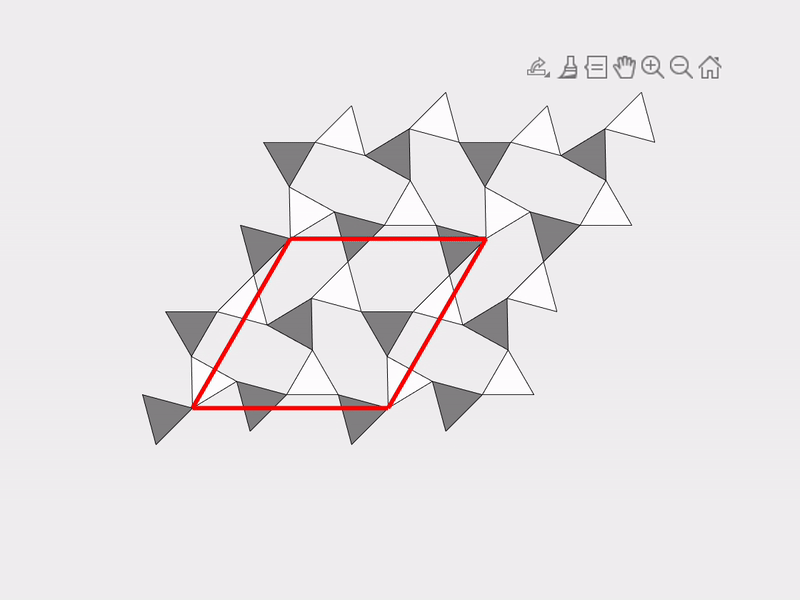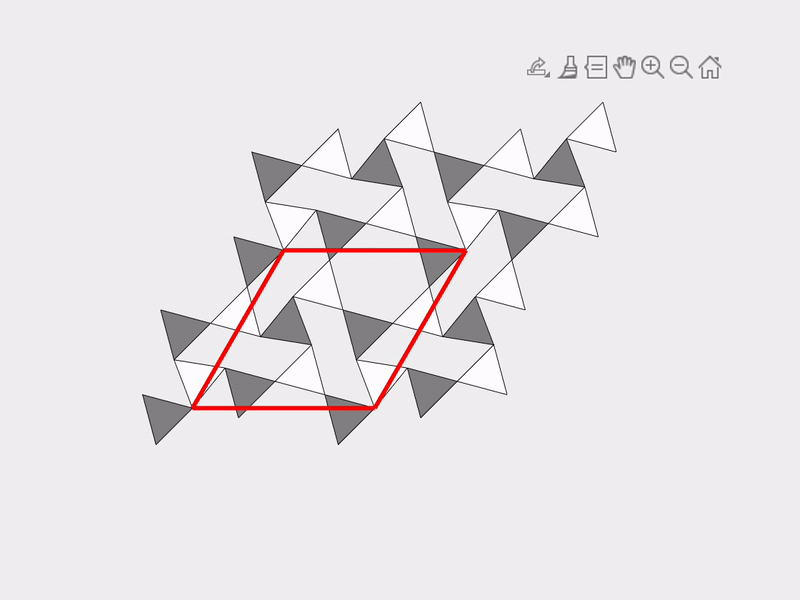This is a joint work with my PhD advisor Robert V. Kohn at Courant Institute. The numerical work is a collaboration with Katia Bertoldi and Bolei Deng.

• Higher-order rigid bar joint frameworks with applications to tensegrity structures

Bar-joint frameworks are widely used to study the structural behavior of interconnected systems. A central problem in these frameworks is to determine whether a framework is locally rigid, meaning that every edge-length-preserving motion is a rigid-body motion. There are several sufficient conditions: the strongest is first-order rigidity, where small deformations immediately change bar lengths, while a weaker notion is prestress stability, in which rigidity arises under specific internal tensions.

Still weaker notions exist, in which bar lengths change only at higher order, making such frameworks mechanically "shaky." We use the term higher-order rigid to describe frameworks that are rigid but not first-order rigid. One prominent type of higher-order rigid framework is the class of tensegrity structures -- rigid assemblies of bars and cables stabilized by self-stress. These tensegrity structures are closely related to prestress stability and enable lightweight, adaptive designs such as NASA’s Superball Bot, which can absorb complex impact loads and traverse rough terrain.

Yet such frameworks are rare. Known examples are usually hand-crafted and rely on special symmetries, such as parallel bars, repeated edge lengths, or coplanar vertices. We have developed a systematic approach to constructing higher-order rigid frameworks. Our findings show that prestress-stable frameworks, rather than being rare, arise robustly as solutions to a simple optimization problem.

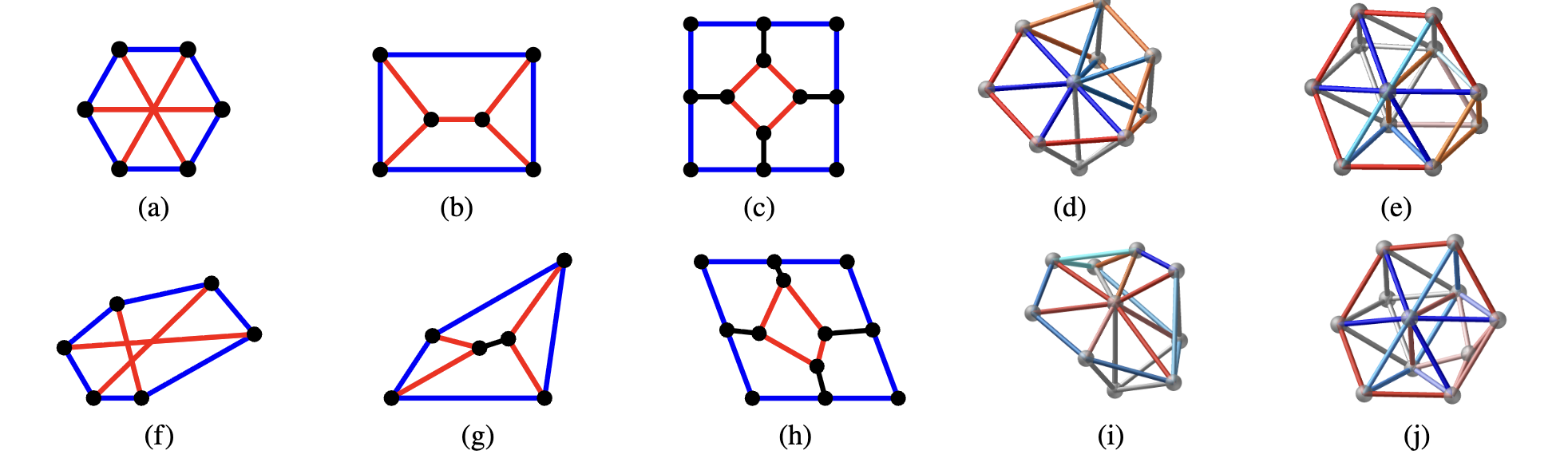This is a joint work with Miranda Holmes-Cerfon and Christian D Santangelo.

Another research interest of mine is related to the singularity of bar frameworks. Singular and flexible frameworks are valuable in robotics, as they enable transitions between distinct kinematic configurations without complex reconfiguration. However, such structures are as rare as higher-order rigid frameworks. To address this, we have developed a systematic constrained saddle-search approach for constructing these singular and flexible frameworks.

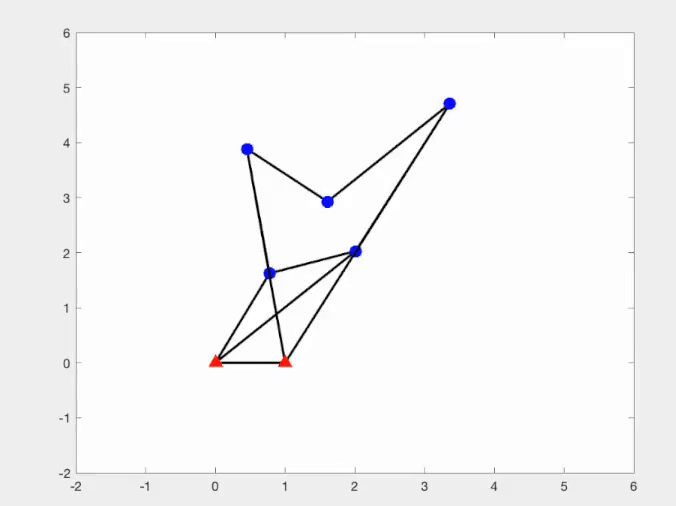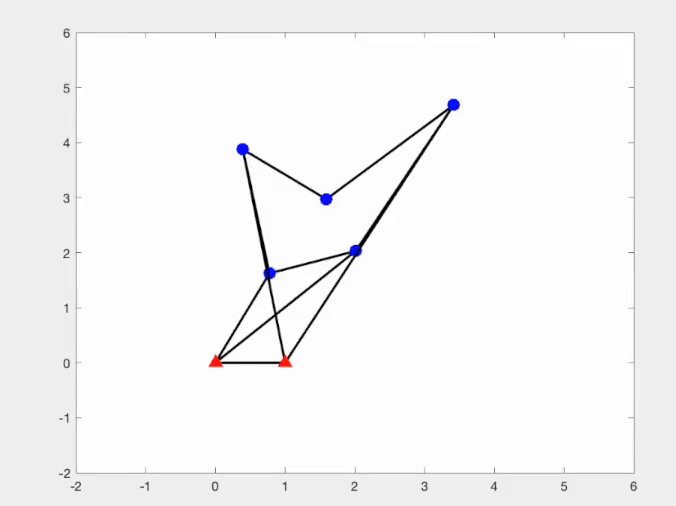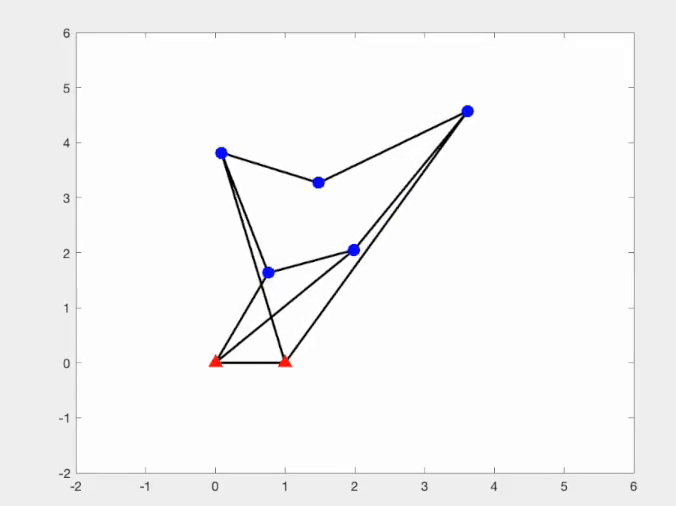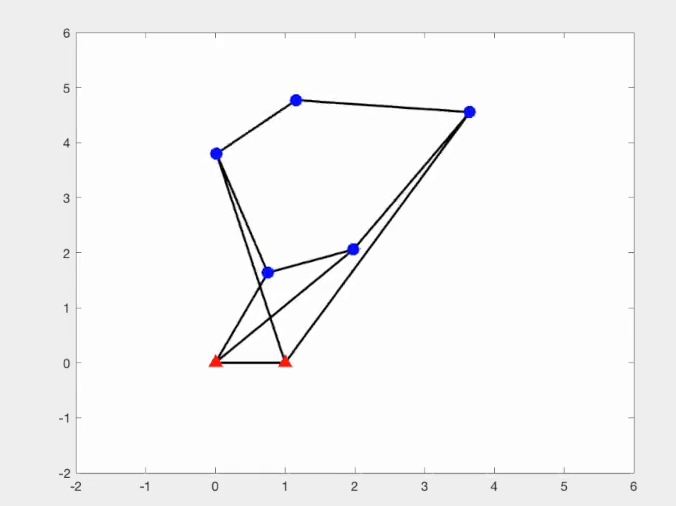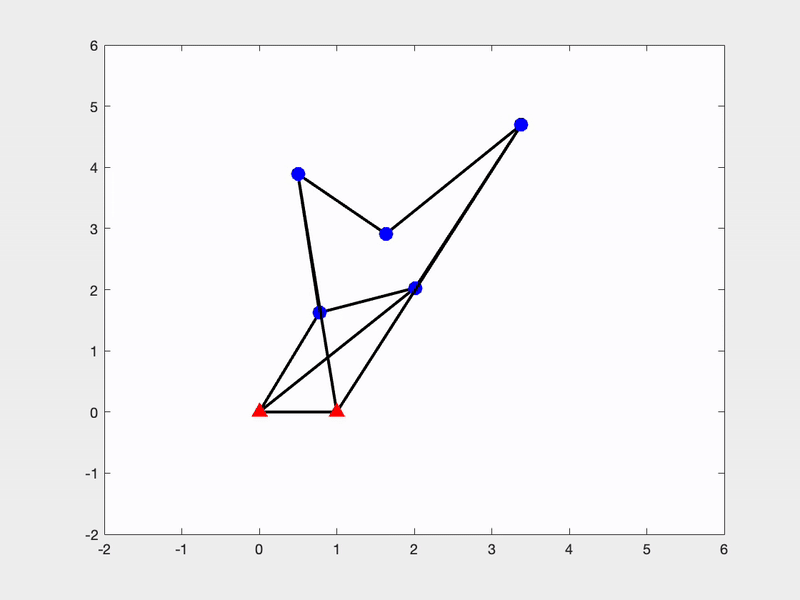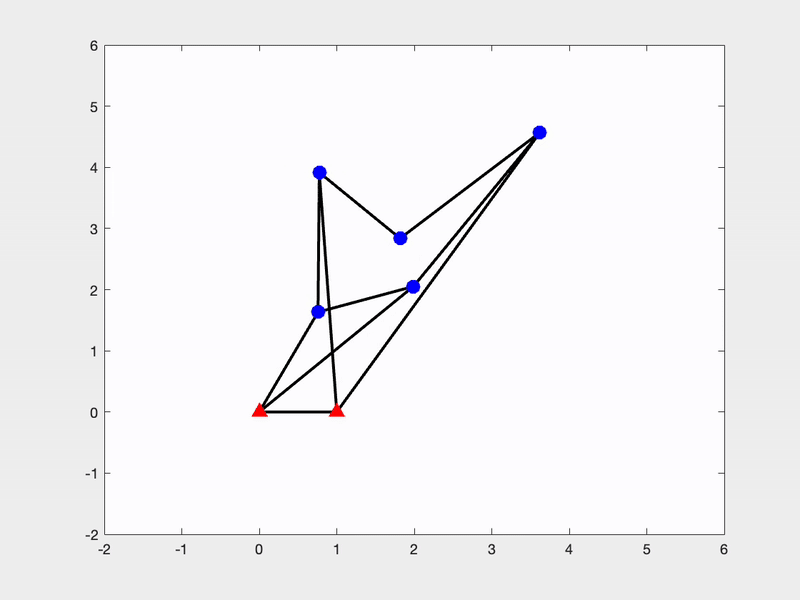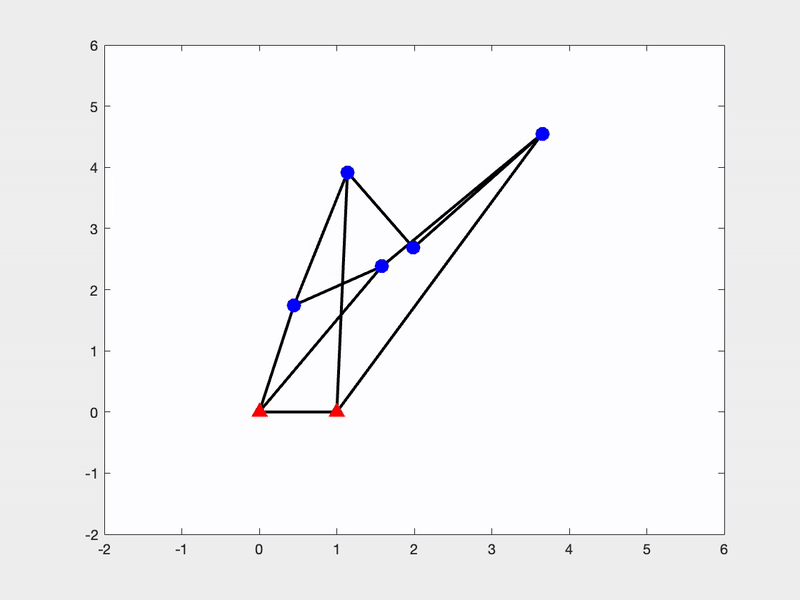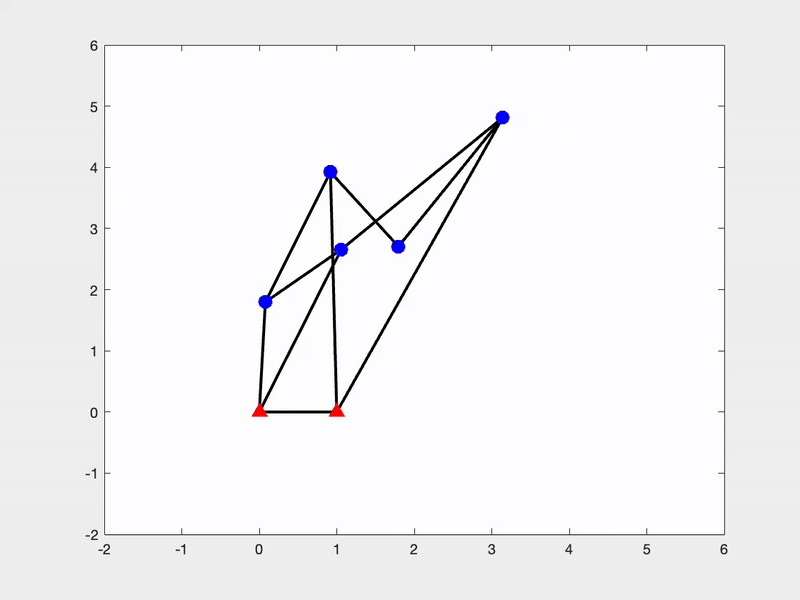This is a joint work with Miranda Holmes-Cerfon, Christian D Santangelo and my student Mihnea Leonte at Columbia University. The code of our constrained saddle search approach to construct singular and flexible bar framework can be found here.

• Pseudo-magnetism in the slowly-strained discrete honeycomb lattice

Honeycomb lattices, underlying 2D materials like graphene, possess special points in their band structures known as Dirac points, where two dispersion surfaces intersect conically . Near these points, the electronic or wave dynamics are governed by an effective two-dimensional Dirac operator. The fact that wavepackets evolve under these effective dynamics is key to understanding the remarkable electronic properties of graphene and selected materials.

In photonic crystals, a remarkable feature arises when the lattice is strained: slowly-varying non-uniform deformations generate effective pseudo-magnetic potentials that alter the band structure and, in turn, the wave propagation. In particular, the slowly-varying quadratic displacement is predicted to generate a Landau gauge for a constant magnetic field. This, in turn, gives rise to Landau levels, which appear in the band structure as flat energy bands. Flat bands imply vanishing group velocity; wavepackets supported on them remain localized rather than spreading, with their energy effectively trapped in the lattice. This phenomenon has been confirmed experimentally.

Motivated by observations in photonic strained honeycomb lattices, we analyze slowly strained honeycomb lattices within a discrete tight-binding model. We use a formal discrete multiscale expansion and derive an effective 2D magnetic Dirac operator for general deformations, which agrees with predictions from the photonic and electronic settings. We also prove the first rigorous convergence result of the discrete multiscale expansion for truncated Landau-gauge deformations with bounded gradients.

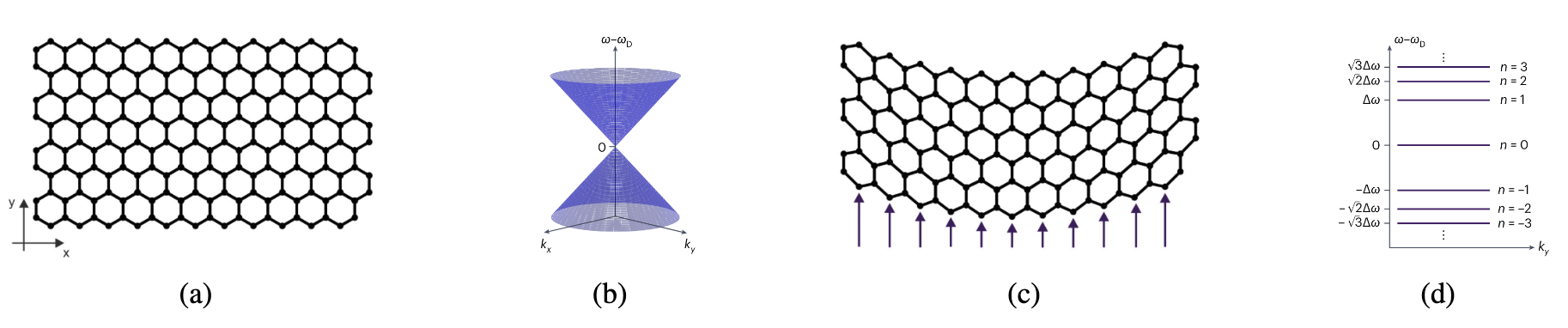This is a joint work with Michael I. Weinstein.